Constraint Solvers¶

Commutation Constraints¶

qecc.solve_commutation_constraints(commutation_constraints=[], anticommutation_constraints=[], search_in_gens=None, search_in_set=None)[source]¶

Given commutation constraints on a Pauli operator, yields an iterator onto all solutions of those constraints.

Parameters:

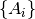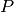commutation_constraints – A list of operators $\{A_i\}$ such that each solution $P$ yielded by this function must satisfy $[A_i, P] = 0$ for all $i$ .
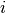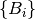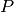anticommutation_constraints – A list of operators $\{B_i\}$ such that each solution $P$ yielded by this function must satisfy 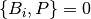$\{B_i, P\} = 0$ for all $i$ .
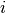search_in_gens – A list of operators 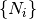$\{N_i\}$ that generate the group in which to search for solutions. If None, defaults to the elementary generators of the pc.Pauli group on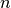 $n$ qubits, where 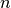$n$ is given by the length of the commutation and anticommutation constraints.
search_in_set – An iterable of operators to which the search for satisfying assignments is restricted. This differs from search_in_gens in that it specifies the entire set, not a generating set. When this parameter is specified, a brute-force search is executed. Use only when the search set is small, and cannot be expressed using its generating set.

Returns:

An iterator it such that list(it) contains all operators within the group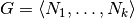 $G = \langle N_1, \dots, N_k \rangle$ given by search_in_gens, consistent with the commutation and anticommutation constraints.

This function is based on finding the generators of the centralizer groups of each commutation constraint, and is thus faster than a predicate-based search over the entire group of interest. The resulting iterator can be used in conjunction with other filters, however.

>>> import qecc as q
>>> list(q.solve_commutation_constraints(q.PauliList('XXI', 'IZZ', 'IYI'), q.PauliList('YIY')))
[i^0 XII, i^0 IIZ, i^0 YYX, i^0 ZYY]
>>> from itertools import ifilter
>>> list(ifilter(lambda P: P.wt <= 2, q.solve_commutation_constraints(q.PauliList('XXI', 'IZZ', 'IYI'), q.PauliList('YIY'))))
[i^0 XII, i^0 IIZ]