Binary Symplectic Form¶
Introduction¶
The qecc package provides support for elements of the Pauli and Clifford groups in
binary symplectic form, including support for algorithms acting on these representations.
Note that all classes and functions documented here depend on the numpy package. For
more information on the binary symplectic representation, read [CRSS96], Section 2.
qecc.BinarySymplecticVector: Binary symplectic representation of Pauli group elements¶
The class qecc.BinarySymplecticVector provides a means of representing elements of the
Pauli group (neglecting global phases) using binary vectors  and
and 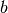 such that an
element
such that an
element 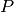 of the Pauli group acting on
of the Pauli group acting on 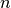 qubits is
qubits is 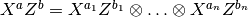 . Binary symplectic vectors can be obtained from a single binary
list, two binary lists, or converted from another Pauli instance (removing the phase):
. Binary symplectic vectors can be obtained from a single binary
list, two binary lists, or converted from another Pauli instance (removing the phase):
>>> import qecc as q
>>> a=[1, 0, 1]; b=[0, 1, 1]
>>> q.BinarySymplecticVector(a,b)==q.BinarySymplecticVector(a+b)
True
>>> import qecc as q
>>> a=[1, 0, 1]; b=[0, 1, 1]
>>> q.BinarySymplecticVector(a,b)
( 1 0 1 | 0 1 1 )
>>> import qecc as q
>>> q.Pauli('XYIYIIZ',2).as_bsv()
( 1 1 0 1 0 0 0 | 0 1 0 1 0 0 1 )
Class Reference¶
-
class
qecc.BinarySymplecticVector(*args)[source]¶ Encapsulates a binary symplectic vector representing an element of the Pauli group on
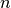 qubits.
qubits.A new
BinarySymplecticVectorcan be constructed using either a single NumPy array containing both the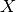 and
and 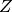 parts of the
binary symplectic vector. Alternatively, a new vector can be instantiated
using two NumPy arrays. For example, the following two invocations are
equivalent:
parts of the
binary symplectic vector. Alternatively, a new vector can be instantiated
using two NumPy arrays. For example, the following two invocations are
equivalent:>>> import qecc >>> import numpy as np >>> bsv = qecc.BinarySymplecticVector(np.array([1, 0, 0, 0, 0, 0])) >>> bsv = qecc.BinarySymplecticVector(np.array([1, 0, 0]), np.array([0, 0, 0]))
The
lenof aBinarySymplecticVectoris defined as the number of qubits upon which the represented Pauli operator acts, and is thus half of the length of a single array containing the same data.-
x¶ Array containing the
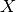 part of the binary symplectic vector.
part of the binary symplectic vector.Return type: numpy.ndarray, shape(2 * nq, ).>>> import qecc as q >>> q.BinarySymplecticVector([1,0,0,0,1,0]).x array([1, 0, 0])
-
z¶ Array containing the
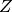 part of the binary symplectic vector.
part of the binary symplectic vector.Return type: numpy.ndarray, shape(nq, ).>>> import qecc as q >>> q.BinarySymplecticVector([1,0,0,0,1,0]).z array([0, 1, 0])
-
copy()[source]¶ Returns a copy of the binary symplectic vector such that mutations of the copy do not affect this instance. For more details, see the
numpy.ndarray.copy()method.
-
as_pauli()[source]¶ Returns an instance of
qecc.Paulirepresenting the same Pauli operator as this vector. Note that phase information is not preserved by the binary symplectic representation of the Pauli group, and soP.as_bsv().as_pauli()need not equalP.>>> import qecc as q >>> pauli_with_phase=q.Pauli('IXXYZ',2) >>> pauli_with_phase.as_bsv().as_pauli() i^0 IXXYZ
-
Utility Functions¶
-
qecc.all_pauli_bsvs(nq)[source]¶ Lists all the Paulis on
nqqubits according to their binary symplectic representations.Parameters: nq (int) – Number of qubits. Returns: an iterator that yields the binary symplectic representations of each element of the Pauli group 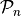 .
.>>> list(all_pauli_bsvs(1)) [( 0 | 0 ), ( 0 | 1 ), ( 1 | 0 ), ( 1 | 1 )]
-
qecc.constrained_set(pauli_array_input, logical_array_input)[source]¶ Given a set of constraints of the form
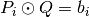 , with
each
, with
each 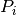 a Pauli operator and each
a Pauli operator and each 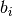 a bit, yields an
iterator onto Pauli operators
a bit, yields an
iterator onto Pauli operators 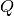 such that all constraints are
satisfied.
such that all constraints are
satisfied.Parameters: - pauli_array_input (
listofqecc.Pauliinstances.) – Constraint operators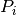 .
. - logical_array_input (
numpy.ndarrayof dtype=int and shape(len(pauli_array_input), ).) – Constraint values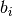 .
.
>>> import qecc as q >>> list(q.constrained_set(map(lambda s: q.Pauli(s).as_bsv(), ['XY','ZZ']),[1,0])) [( 0 0 | 0 1 ), ( 0 0 | 1 0 ), ( 1 1 | 0 0 ), ( 1 1 | 1 1 )]
- pauli_array_input (
-
qecc.commute(bsv1, bsv2)[source]¶ Returns True if bsv1 and bsv2 commute by evaluating the symplectic inner product.
Return type: bool
-
qecc.xz_switch(bsv)[source]¶ Given a
qecc.BinarySymplecticVector, returns a new vector whose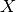 and
and 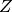 parts have been swapped.
parts have been swapped.
qecc.BinarySymplecticMatrix - Binary symplectic representation of Clifford group elements¶
Class Reference¶
-
class
qecc.BinarySymplecticMatrix(*args)[source]¶ Encapsulates a binary symplectic matrix representing an element of the Clifford group on
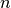 qubits.
qubits.A new
BinarySymplecticMatrixcan be constructed using either a single NumPy 2-D array containing the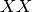 ,
, 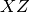 ,
, 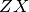 , and
, and 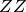 parts of the binary symplectic matrix. Alternatively, a new matrix can be instantiated
using four NumPy arrays. For example, the following two invocations are
equivalent:
parts of the binary symplectic matrix. Alternatively, a new matrix can be instantiated
using four NumPy arrays. For example, the following two invocations are
equivalent:>>> import qecc >>> import numpy as np >>> bsm = qecc.BinarySymplecticMatrix(np.array([[1, 0, 0, 0],[1, 1, 0, 0],[0, 0, 1, 1],[0, 0, 0, 1]])) >>> bsm = qecc.BinarySymplecticMatrix(np.array([[1, 0],[1, 1]]), np.array([[0, 0],[0, 0]]), np.array([[0, 0],[0, 0]]), np.array([[1, 1],[0, 1]]))
-
nq¶ Returns the number of qubits that the binary symplectic matrix acts upon.
-
xc¶ Returns the left half of a binary symplectic matrix.
-
zc¶ Returns the right half of a binary symplectic matrix.
-
xr¶ Returns the top half of a binary symplectic matrix.
-
zr¶ Returns the bottom half of a binary symplectic matrix.
-
xx¶ Returns the upper-left quadrant of a binary symplectic matrix.
-
xz¶ Returns the upper-right quadrant of a binary symplectic matrix.
-
zx¶ Returns the lower-left quadrant of a binary symplectic matrix.
-
zz¶ Returns the lower-right quadrant of a binary symplectic matrix.
-
left_H(j)[source]¶ Multiplies on the left by a Hadamard gate on the
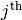 qubit. This method acts in-place, as opposed to acting on a copy of the
binary symplectic matrix. In order to preserve the original matrix,
use the
qubit. This method acts in-place, as opposed to acting on a copy of the
binary symplectic matrix. In order to preserve the original matrix,
use the copy()method:>>> new_bsm = bsm.copy().left_H(idx)
-
right_H(j)[source]¶ Multiplies on the right by a Hadamard gate on the
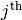 qubit. See
qubit. See left_H()for more details.
-
right_H_all()[source]¶ Multiplies on the right by a Hadamard gate on each qubit. See
left_H()for more details.
-
left_SWAP(j, k)[source]¶ Multiplies on the left by a SWAP gate between the
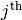 and
and 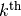 qubits. This method acts in-place, as opposed
to acting on a copy of the binary symplectic matrix. In order to
preserve the original matrix, use the
qubits. This method acts in-place, as opposed
to acting on a copy of the binary symplectic matrix. In order to
preserve the original matrix, use the copy()method:>>> new_bsm = bsm.copy().left_SWAP(j, k)
-
right_SWAP(j, k)[source]¶ Multiplies on the right by a SWAP gate between the
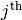 and
and 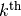 qubits. See
qubits. See left_SWAP()for more details.
-
left_CNOT(c, t)[source]¶ Multiplies on the left by a CNOT gate controlled by the
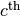 qubit and targeting the
qubit and targeting the 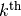 qubit. This method acts in-place, as opposed to acting on a copy of the
binary symplectic matrix. In order to preserve the original matrix, use
the
qubit. This method acts in-place, as opposed to acting on a copy of the
binary symplectic matrix. In order to preserve the original matrix, use
the copy()method:>>> new_bsm = bsm.copy().left_CNOT(c, t)
-
right_CNOT(c, t)[source]¶ Multiplies on the right by a CNOT gate controlled by the
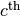 qubit and targeting the
qubit and targeting the 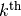 qubit. For more details, see
qubit. For more details, see left_CNOT().
-
left_R_pi4(i)[source]¶ Multiplies on the left by an
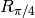 gate acting on the
gate acting on the
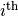 qubit. This method acts in-place, as opposed to
acting on a copy of the binary symplectic matrix. In order to preserve
the original matrix, use the
qubit. This method acts in-place, as opposed to
acting on a copy of the binary symplectic matrix. In order to preserve
the original matrix, use the copy()method:>>> new_bsm = bsm.copy().left_R_pi4(c, t)
-
right_R_pi4(i)[source]¶ Multiplies on the right by an
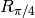 gate acting on the
gate acting on the
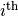 qubit. For more details, see
qubit. For more details, see
left_R_pi4().
-
left_CZ(c1, c2)[source]¶ Multiplies on the left by an controlled-
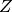 gate acting between
the
gate acting between
the 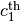 and
and 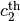 qubits. This
method acts in-place, as opposed to acting on a copy of the binary
symplectic matrix. In order to preserve the original matrix, use the
qubits. This
method acts in-place, as opposed to acting on a copy of the binary
symplectic matrix. In order to preserve the original matrix, use the
copy()method:>>> new_bsm = bsm.copy().left_CZ(c, t)
-
right_CZ(c1, c2)[source]¶ Multiplies on the right by an controlled-
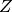 gate acting between
the
gate acting between
the 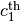 and
and 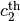 qubits. For more
details, see
qubits. For more
details, see left_CZ().
-
inv(check_validity=True)[source]¶ Returns the inverse of this binary symplectic matrix, assuming that this matrix represents a valid Clifford gate.
Note that if the matrix
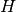 does not represent a valid Clifford,
this method will return a matrix
does not represent a valid Clifford,
this method will return a matrix 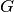 such that
such that 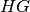 is
not the identity matrix.
is
not the identity matrix.Parameters: check_validity (bool) – If True, then the matrix is first checked to ensure that it is a valid Clifford.Raises: qecc.InvalidCliffordErrorifcheck_validityisTrueand the binary symplectic matrix being inverted does not represent a valid Clifford group element.
-
as_clifford(check_validity=True)[source]¶ Converts this binary symplectic matrix into a Clifford representation.
Parameters: check_validity (bool) – If True, then the matrix is first checked to ensure that it is a valid Clifford.Return type: qecc.CliffordReturns: The same gate as this binary symplectic matrix, represented as an instance of qecc.Clifford.
-
is_valid()[source]¶ Checks the satisfaction of the symplectic condition on a
qecc.BinarySymplecticMatrixobject.
-
Utility Functions¶
-
qecc.bsmzeros(nq)[source]¶ Returns a binary symplectic matrix on
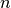 qubits, initialized to all
zeros.
qubits, initialized to all
zeros.Parameters: nq (int) – Number of qubits that the created matrix will act upon. Returns: A binary symplectic matrix containing all zeros. Return type: BinarySymplecticMatrix
-
qecc.array_to_pauli(bsv_array)[source]¶ Function wrapper for type conversion from binary symplectic vector to
qecc.Pauli. Seeqecc.BinarySymplecticVector.as_pauli().
 of this
vector with another vector. Letting
of this
vector with another vector. Letting 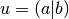 and
and
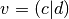 ,
, 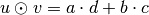 .
.