Pauli and Clifford Groups¶
qecc.Pauli: Class representing Pauli group elements¶
The class qecc.Pauli is used to represent elements of the Pauli group
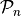 on
on 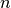 qubits. Instances can be constructed by
specifying strings of
qubits. Instances can be constructed by
specifying strings of I, X, Y and Z, corresponding to the
specification of an operator in the Pauli group.
>>> import qecc as q
>>> P = q.Pauli('X')
>>> print P
i^0 X
>>> Q = q.Pauli('XZZXI')
>>> print Q
i^0 XZZXI
>>> R = q.Pauli('XYZ')
>>> print R
i^0 XYZ
Additionaly, a phase can be provided. Since only integer powers of 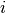 are
allowed as phases, the phase of a
are
allowed as phases, the phase of a qecc.Pauli instance is represented
by an integer in range(4). Any other integer is converted to an integer
in that range that is equivalent mod 4.
>>> print q.Pauli('X', 2)
i^2 X
The qecc.Pauli class supports multiplication, tensor products and
negation by the *, & and - operators, respectively.
>>> import qecc
>>> P = qecc.Pauli('X')
>>> Q = qecc.Pauli('Y')
>>> P * Q
i^1 Z
>>> P & Q
i^0 XY
>>> -P * Q
i^3 Z
Using these operators, it is straightforward to construct instances of
qecc.Pauli from existing instances. To make this easier, QuaEC provides
single-qubit operators I, X, Y and Z.
>>> from qecc import I, X, Y, Z
>>> print q.Pauli('XZZXI') & I
i^0 XZZXII
Additionally, instances of qecc.Pauli can be tested for equality.
>>> -P * Q == P * -Q
True
>>> P * Q != Q * P
True
The length of a qecc.Pauli is defined as the number of qubits it acts
upon.
>>> print len(qecc.Pauli('XYZI'))
4
This information is also exposed as the property nq.
>>> print qecc.Pauli('XYZI').nq
4
Class Reference¶
-
class
qecc.Pauli(operator, phase=0)[source]¶ Class representing an element of the Pauli group on
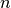 qubits.
qubits.Parameters: -
nq¶ Returns the number of qubits upon which this Pauli operator acts.
-
wt¶ Measures the weight of a given Pauli.
Return type: int (between 0 and the number of qubits on which the Pauli is defined) Returns: The number of qubits on which the represented Pauli operator is supported.
-
str_sparse(incl_ph=True)[source]¶ Returns a compact representation for
qecc.Pauliobjects, for those having support on a small number of qubits of a large register.
-
tens(other)[source]¶ Concatenates the op strings of two Paulis, and multiplies their phases, to produce the Kronecker product of the two.
Parameters: other (qecc.Pauli) – Pauli operator 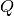 to be tensored with this instance.
to be tensored with this instance.Returns: An instance representing 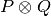 , where
, where 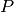 is the Pauli operator represented by this instance.
is the Pauli operator represented by this instance.
-
set_phase(ph=0)[source]¶ Returns a
qecc.Pauliobject having the same operator as the input, with a specified phase (usually used to erase phases).
-
mul_phase(ph)[source]¶ Increments the phase of this Pauli by
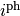 .
.Parameters: ph (int) – Amount the phase is to be incremented by. Returns: This instance.
-
permute_op(perm)[source]¶ Returns a new
qecc.Pauliinstance whose operator part is related to the operator part of this Pauli, so that is mapped to
is mapped to 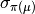 for some
permutation
for some
permutation  of the objects
of the objects 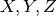 .
.For example:
>>> import qecc as q >>> P = q.Pauli('XYZXYZ') >>> print P.permute_op('ZXY') i^0 ZXYZXY
Note that the result is not guaranteed to be the result of a Clifford operator acting on this Pauli, as permutation may not respect the phases introduced by taking products. For example:
>>> import qecc as q >>> P = q.Pauli('XYZ') >>> Q = q.Pauli('YYZ') >>> P * Q i^1 ZII >>> Pp = P.permute_op('ZYX') >>> Qp = Q.permute_op('ZYX') >>> Pp * Qp i^3 XII
Parameters: perm (list) – A list indicating which permutation is to be performed. Returns: A new instance Q of qecc.Paulithat is related to this instance by a permutation of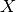 ,
, 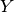 and
and
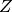 .
.
-
as_gens()[source]¶ Expresses an input Pauli in terms of the elementary generators
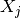 and
and 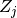 , stripping off phases.
, stripping off phases.Return type: list of qecc.Pauliinstances.
-
as_bsv()[source]¶ Converts the given Pauli to a binary symplectic vector, discarding phase information.
Returns: A binary symplectic vector representing this Pauli operator. Return type: BinarySymplecticVector
-
as_circuit()[source]¶ Transforms an n-qubit Pauli to a serial circuit on n qubits. Neglects global phases.
Return type: qecc.Circuit
-
as_unitary()[source]¶ Returns a
numpy.ndarraycontaining a unitary matrix representation of this Pauli operator.Raises a
RuntimeErrorif NumPy cannot be imported.
-
as_clifford()[source]¶ Converts a Pauli into a Clifford which changes the signs of input Paulis. :returns: A Clifford representing conjugation by this Pauli operator. :rtype:
qecc.Clifford
-
static
from_sparse(sparse_pauli, nq=None)[source]¶ Given a dictionary from non-negative integers to single-qubit Pauli operators or strings representing single-qubit Pauli operators, creates a new instance of
qecc.Paulirepresenting the input.>>> from qecc import Pauli, X, Y, Z >>> print Pauli.from_sparse({3: X, 5: X, 7: Z}, nq=12) i^0 X[3] X[5] Z[7]
Parameters:
-
static
from_clifford(cliff_in)[source]¶ Tests an input Clifford
cliff_into determine if it is, in fact, a Pauli. If so, it outputs the Pauli. If not, it raises an error.Parameters: cliff_in – Representation of Clifford operator to be converted, if possible. Return type: qecc.PauliExample:
>>> import qecc as q >>> cliff = q.Clifford([q.Pauli('XI',2),q.Pauli('IX')], map(q.Pauli,['ZI','IZ'])) >>> q.Pauli.from_clifford(cliff) i^0 ZI
Converting a Pauli into a Clifford and back again will erase the phase:
>>> import qecc as q >>> paul = q.Pauli('YZ',3) >>> cliff = paul.as_clifford() >>> q.Pauli.from_clifford(cliff) i^0 YZ
-
static
from_string(bitstring, p_1)[source]¶ Creates a multi-qubit Pauli using a bitstring and a one-qubit Pauli, by replacing all instances of 1 in the bitstring with the appropriate Pauli, and replacing all instances of 0 with the identity.
Parameters: Returns: a phaseless Pauli from a bitstring. The intended use of this function is as a quick means of specifying binary Paulis. p_1 is the one_qubit Pauli that a ‘1’ represents.
Return type: Example:
>>> import qecc as q >>> bitstring = '101110111100' >>> p_1 = q.Pauli('X') >>> q.Pauli.from_string(bitstring, p_1) i^0 XIXXXIXXXXII
-
reg_wt(**kwargs)[source]¶ Produces the number of qubits within a subset of the register on which the Pauli in question acts non-trivially.
Parameters: region (tuple) – a tuple containing the indices on which the weight is to be evaluated. Returns: the number of qubits in the sub-register on which the Pauli selfdoes not act as the identity.
-
cust_wt(char)[source]¶ Produces the number of qubits on which an input Pauli acts as a specified single-qubit Pauli.
Parameters: char (str) – a single-letter string containing an I, X, Y or Z. Returns: the number of qubits in the Pauli selfwhich are acted upon by the single-qubit operatorchar.
-
ct()[source]¶ The conjugate transpose of this Pauli operator.
Return type: an instance of the qecc.Pauliclass.
-
centralizer_gens(group_gens=None)[source]¶ Returns the generators of the centralizer group
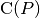 ,
where
,
where 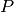 is the Pauli operator represented by this instance.
If
is the Pauli operator represented by this instance.
If group_gensis specified,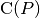 is taken to be
a subgroup of the group
is taken to be
a subgroup of the group 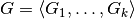 ,
where
,
where 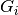 is the
is the 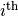 element of
element of
group_gens.Parameters: group_gens (list of qecc.Pauliinstances) – EitherNoneor a list of generators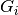 .
If not
.
If not None, the returned centralizer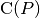 is
a subgroup of the group
is
a subgroup of the group 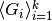 .
.Returns: A list of elements 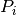 of the Pauli group such that
of the Pauli group such that
 , where
, where
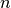 is the number of unique generators of the centralizer.
is the number of unique generators of the centralizer.
-
Iterating Over Groups and Subgroups¶
-
qecc.pauli_group(nq)[source]¶ Generates an iterator onto the Pauli group of
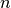 qubits,
where
qubits,
where 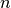 is given as the argument nq.
is given as the argument nq.Parameters: nq (int) – The number of qubits acted upon by the returned Pauli group. Returns: An iterator such that list(pauli_group(nq))produces a list of all possible Pauli operators onnqqubits.
Utility Functions¶
-
qecc.com(P, Q)[source]¶ Given two elements P and Q of a Pauli group, returns 0 if
![[P, Q] = 0](_images/math/e2434330d1ddaa027616785290daa928b97e3522.png) and returns 1 if
and returns 1 if 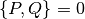 .
.Parameters: - P (qecc.Pauli) – Representation of
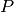 .
. - Q (qecc.Pauli) – Representation of
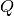 .
.
Returns: 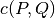 .
.Return type: - P (qecc.Pauli) – Representation of
-
qecc.elem_gens(nq)[source]¶ Produces all weight-one
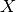 and
and 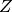 operators on nq qubits.
For example,
operators on nq qubits.
For example,>>> import qecc as q >>> Xgens, Zgens = q.elem_gens(2) >>> print Xgens[1] i^0 IX
Parameters: nq (int) – Number of qubits for each returned operator. Returns: a tuple of two lists, containing 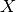 and
and 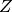 generators, respectively.
generators, respectively.
-
qecc.eye_p(nq)[source]¶ Given a number of qubits, returns the identity Pauli on that many qubits.
Parameters: nq (int) – Number of qubits upon which the returned Pauli acts. Return type: qecc.PauliReturns: A Pauli operator acting as the identity on each of nqqubits.
Searching Over Pauli Group Elements¶
QuaEC provides useful tools for searching over elements of the Pauli group. A few particlar searches are provided built-in, while other searches can be efficiently built using the predicates described in Predicates and Filters.
-
qecc.is_in_normalizer(pauli, stab)[source]¶ Given an element
pauliof a Pauli group and the generatorsstabof a stabilizer group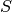 , returns True if and only if
, returns True if and only if
pauliis in the normalizer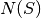 .
.
-
qecc.mutually_commuting_sets(n_elems, n_bits=None, group_gens=None, exclude=None)[source]¶ Yields an iterator onto tuples representing mutually commuting sets of
n_elemsindependent Pauli operators, excluding the identity Pauli.Parameters: - n_elems (int) – The number of mutually commuting Pauli operators to include in each tuple.
- n_bits (int) – The number of qubits on which each Pauli operator
considered by this iterator acts. If
None, defaults to the number of qubits on which the first element ofgroup_gensacts. - group_gens (
Noneor a sequence ofqecc.Pauliinstances) – The generators of the group in which to search for mutually commuting Pauli operators. Defaults to the elementary generators of the Pauli group onn_bitsqubits. - exclude (
Noneor a sequence ofqecc.Pauliinstances) – If notNone, the iterator will omit from its search any operators in the group generated byexclude.
qecc.Clifford: Class representing Clifford group elements¶
Elements of the automorphism group of the Pauli group (known as the Clifford
group) are represented by the class qecc.Clifford. Instances of
Clifford are constructed by specifying the mappings of the generators of
the Pauli group, such that the action of a Clifford instance is defined
for all input Pauli group elements.
>>> import qecc as q
>>> C = q.Clifford(['XX', 'IX'], ['ZI', 'ZZ'])
>>> print C
XI |-> +XX
IX |-> +IX
ZI |-> +ZI
IZ |-> +ZZ
Also, the results of an element of the Clifford group can be left partially
unspecified, using the singleton qecc.Unspecified:
>>> import qecc as q
>>> print q.Clifford(['IZ','XZ'],['XI',q.Unspecified])
XI |-> +IZ
IX |-> +XZ
ZI |-> +XI
IZ |-> Unspecified
Once an instance of qecc.Clifford has been constructed in this way,
its action on elements of the Pauli group can be calculated by calling the
Clifford instance as a function.
>>> from qecc import I, X, Y, Z
>>> C(X & Y)
i^0 YZ
>>> map(C, ['XI', 'IX', 'YI', 'IY', 'ZI', 'IZ'])
[i^0 XX, i^0 IX, i^0 YX, i^0 ZY, i^0 ZI, i^0 ZZ]
Note that in this example, C has converted strings to qecc.Pauli
instances. This is done automatically by qecc.Clifford.
Instances of Clifford can be combined by multiplication (*) and by
tensor products (&). Multiplication of two Clifford instances returns
a new instance representing their composition, while the tensor product returns
a new instance that acts on each register independently.
>>> import qecc as q
>>> C = q.Clifford(['XX', 'IX'], ['ZI', 'ZZ'])
>>> D = q.Clifford(['XI', 'IZ'], ['ZI', 'IX'])
>>> print C * D
XI |-> +XX
IX |-> +ZZ
ZI |-> +ZI
IZ |-> +IX
>>> print C & D
X[0] |-> +X[0] X[1]
X[3] |-> +Z[3]
Z[1] |-> +Z[0] Z[1]
Z[3] |-> +X[3]
Note that in the second example, the printing of the Clifford operator has
switched to a sparse format that suppresses printing lines for qubits that are
not acted upon by the operator (in this case, qubits 1 and 2 are
trivially acted upon by C & D).
As with qecc.Pauli, the length of a qecc.Clifford instance
is defined as the number of qubits on which that instance acts. This information
is also exposed as the property nq.
>>> import qecc as q
>>> C = q.Clifford(['XX', 'IX'], ['ZI', 'ZZ'])
>>> print len(C)
2
>>> print C.nq
2
Class Reference¶
-
class
qecc.Clifford(xbars, zbars)[source]¶ Class representing an element of the Cifford group on
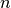 qubits.
qubits.Parameters: - xbars (list of
qecc.Pauliinstances) – A list of operators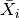 such that the
represented Clifford operation
such that the
represented Clifford operation 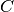 acts as
acts as
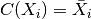 . Note that in order for the represented
operator to be an automorphism, each
. Note that in order for the represented
operator to be an automorphism, each 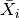 must have phase
either 0 or 2. A warning will result if this condition is not met.
must have phase
either 0 or 2. A warning will result if this condition is not met. - zbars (list of
qecc.Pauliinstances) – Seexbars.
-
nq¶ Returns the number of qubits on which this
qecc.Cliffordobject acts.
-
n_unspecified¶ Returns the number of unspecifed outputs of this
qecc.Cliffordobject.
-
str_sparse()[source]¶ Provides a compact representation for
qecc.Cliffordobjects, intended for use in the case where many of the outputs have small support.
-
is_valid(quiet=True)[source]¶ Returns
Trueif this instance represents a valid automorphism. In particular, this method returnsTrueif all output phase assignments are either 0 or 2, and if all of the commutation relations on its outputs are obeyed. Unspecified outputs are ignored.Parameters: quiet (bool) – If set to True, this method will not print out any information, but will returnTrueorFalseas described above. Otherwise, if the operator is not a valid Clifford operator, diagnostic information will be printed.
-
inv()[source]¶ Calculates the inverse
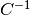 of this Clifford operator
of this Clifford operator
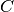 , such that
, such that 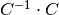 is the identity Clifford.
is the identity Clifford.
-
conjugate_pauli(pauli)[source]¶ Given an instance of
qecc.Paulirepresenting the operator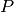 , calculates the mapping
, calculates the mapping
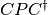 , where
, where 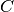 is the operator represented by
this instance.
is the operator represented by
this instance.Parameters: pauli (qecc.Pauli) – Representation of the Pauli operator 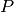 .
.Returns: Representation of the Pauli operator 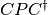 , where
, where 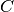 is the Clifford operator
represented by this instance.
is the Clifford operator
represented by this instance.Return type: qecc.Pauli
-
constraint_completions()[source]¶ Yields an iterator onto possible Clifford operators whose outputs agree with this operator for all outputs that are specified. Note that all yielded operators assign the phase 0 to all outputs, by convention.
If this operator is fully specified, the iterator will yield exactly one element, which will be equal to this operator.
For example:
>>> import qecc as q >>> C = q.Clifford([q.Pauli('XI'), q.Pauli('IX')], [q.Unspecified, q.Unspecified]) >>> it = C.constraint_completions() >>> print it.next() XI |-> +XI IX |-> +IX ZI |-> +ZI IZ |-> +IZ >>> print it.next() XI |-> +XI IX |-> +IX ZI |-> +ZI IZ |-> +IY >>> print len(list(C.constraint_completions())) 8
If this operator is not a valid Clifford operator, then this method will raise an
qecc.InvalidCliffordErrorupon iteraton.
-
as_bsm()[source]¶ Returns a representation of the Clifford operator as a binary symplectic matrix.
Return type: qecc.BinarySymplecticMatrix
-
as_unitary()[source]¶ Returns a
numpy.ndarraycontaining a unitary matrix representation of this Clifford operator.Raises a
RuntimeErrorif NumPy cannot be imported.
-
circuit_decomposition(include_pauli=True)[source]¶ Returns a
qecc.Circuitobject consisting of the circuit decomposition of self.as_bsm() and aqecc.Pauliobject which ensures the output phases of theqecc.Cliffordobject are preserved.Parameters: include_pauli (bool) – If True, Pauli locations are added at the end of the returned circuit. If False, the returned Circuit is correct only up to a Pauli operator at the end. Return type: Circuit
- xbars (list of
Alternate Constructors¶
In addition to specifying the outputs of a Clifford operator acting on the
elementary generators of the Pauli group, one can also create a Clifford
instance by specifying the ouput of an operator on an arbitrary generating set.
In particlar, the function qecc.generic_clifford() takes the inputs and outputs
of a given Clifford operator in order to create a qecc.Clifford
instance.
-
qecc.generic_clifford(paulis_in, paulis_out)[source]¶ Given two lists of
qecc.Pauliinstances,paulis_inandpaulis_out, produces an instanceCofqecc.Cliffordsuch thatC(paulis_in[i]) == paulis_out[i]for alliinrange(2 * nq), wherenqis the length of each element of the two lists.Each of
paulis_inandpaulis_outis assumed to be ordered such that the slice[0:nq]produces a list of logical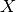 operators, and
such that the slice
operators, and
such that the slice [nq:2*nq]produces the logical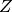 operators.
operators.Parameters: - paulis_in – A list of length
2 * nqlogical Pauli operators specifying the input constraints for the desired Clifford operation. - paulis_out – A list of length
2 * nqlogical Pauli operators specifying the output constraints for the desired Clifford operation.
Returns: A Clifford operator mapping the input constraints to the output constraints.
Return type: - paulis_in – A list of length
Iterators onto the Clifford Group¶
-
qecc.clifford_group(nq, consider_phases=False)[source]¶ Given a number of qubits
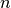 , returns an iterator that produces all
elements of
, returns an iterator that produces all
elements of 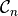 , the Clifford group on
, the Clifford group on 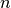 qubits.
qubits.Parameters: - nq (int) – The number of qubits upon which each yielded element will act.
- consider_phases (bool) – If
True, then Clifford operators whose assignments of phases to the generators of the Pauli group differ will be treated as distinct. Otherwise, the yielded elements will be drawn from the group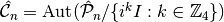 ,
such that the phases of the outputs are not considered.
,
such that the phases of the outputs are not considered.
Common Clifford Gates¶
The qecc package provides support for several common Clifford operators.
These functions can be used to quickly analyze small circuits. For more
extensive circuit support, please see Circuit Manipulation and Simulation.
-
qecc.eye_c(nq)[source]¶ Yields the identity Clifford, defined to map every generator of the Pauli group to itself.
Return type: Clifford
-
qecc.cnot(nq, ctrl, targ)[source]¶ Yields the
nq-qubit CNOT Clifford controlled onctrl, acting a Pauli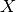 on
on targ.Return type: qecc.Clifford
-
qecc.hadamard(nq, q)[source]¶ Yields the
nq-qubit Clifford, switching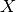 and
and 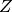 on qubit
on qubit q, yielding a minus sign on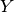 .
.Return type: qecc.Clifford
-
qecc.phase(nq, q)[source]¶ Yields the
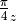 -rotation Clifford, acting on qubit
-rotation Clifford, acting on qubit q.Return type: qecc.Clifford
-
qecc.swap(nq, q1, q2)[source]¶ Yields the swap Clifford, on
nqqubits, which swaps the Pauli generators onq1andq2.Return type: qecc.Clifford
-
qecc.cz(nq, q1, q2)[source]¶ Yields the
nq-qubit C-Z Clifford, acting on qubitsq1andq2.Return type: qecc.Clifford
-
qecc.pauli_gate(pauli)[source]¶ Imports an instance of the
qecc.Pauliclass into theqecc.Cliffordclass, representing a Pauli as a series of sign changes.Return type: qecc.Clifford
 .
.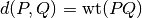 .
.